Question

Write an equation for the line that passes through (-8.5,11) and (5,-2.5)

Answer 1

The equation is y = -x + 2.5

Explanation:

* Lets explain how to solve the problem

- The form of the equation of a line is y = mx + c , where m is the slope

of the line and c is the y-intercept

- The y-intercept means the line intersect the y-axis at point (0 , c)

- The slope of the line which passes through points (x1 , y1) , (x2 , y2)

is
`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

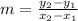
* Lets solve the problem

∵ The line passes through the points (-8.5 , 11) and (5 , -2.5)

- Let point(x1 , y1) = (-8.5 , 11) and point (x2 , y2) = (5 , -2.5)

∴ x1 = -8.5 , x2 = 5 and y1 = 11 , y2 = -2.5

∴
`m=(-2.5-11)/(5-(-8.5))=(-13.5)/(5+8.5)=(-13.5)/(13.5)=-1`

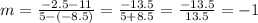
∴ The slope of the line is -1

∵ y = mx + c

∴ y = -x + c

- To find c substitute x and y in the equation by the coordinates of

one of the two points

∵ Point (5 , -2.5) lies on the line

∴ x = 5 at y = -2.5

∵ y = -x + c

∴ -2.5 = -(5) + c

∴ -2.5 = -5 + c

- Add 5 to both sides

∴ c = 2.5

∴ y = -x + 2.5

* The equation is y = -x + 2.5