Question

the gestation time for cows is normally distributed with a mean of 284 days and a standard deviation of 12 days. at a local Ranch over the course of a year they're 820 calf births. of these how many would be expected to have a gestation time of less than 270 days​

Answer 1

100 calfs

Explanation:

We must calculate the probability that the cows have a gestation time of less than 270 days. If X represents the gestation time of a randomly selected cow, then we look for:

`P (X <270)`

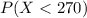
Acora we calculate the Z-score

`Z=(X-\mu)/(\sigma)`

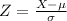
In this case

`\mu=284\ days\\\\\sigma = 12\ days`

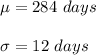
So

`P (X <270) =P ((X-\mu)/(\sigma) <(270-284)/(12))=P(Z<-1.167)`

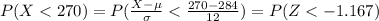
Looking in the normal standard table we have to

`P(Z<-1.167)=0.1216`

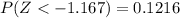
Finally, the expected number of calf "E" that will have a gestation time of less than 270 days is:

`E=820*P (X <270)\\\\E=820*0.1216`

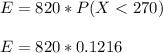
E=99.71≈100 Calfs