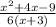Question

What is the simplified form of the quantity of x plus 7, all over the quantity of 6 − the quantity of x plus 5, all over the quantity of x plus 3?

Answer 1

Explanation:

[ (x + 7) / 6 ] − [ (x + 5) / (x + 3) ]

First, we must find the common denominator. In this case, that's 6 (x+3). Multiply the first fraction by (x+3)/(x+3) and the second fraction by 6/6.

[ (x + 7)(x + 3) / (6 (x + 3)) ] − [ 6 (x + 5) / (6 (x + 3)) ]

Now distribute the numerators:

[ (x² + 10x + 21) / (6 (x + 3)) ] − [ (6x + 30) / (6 (x + 3)) ]

Now we combine the fractions:

((x² + 10x + 21) − (6x + 30)) / (6 (x + 3))

(x² + 10x + 21 − 6x − 30) / (6 (x + 3))

(x² + 4x − 9) / (6 (x + 3))

So the simplified form is:

`(x^(2) + 4x - 9)/(6 (x + 3))`