Question

PLEASE HELP ASAP!!!! Thanks!!

The sum of the lengths of two opposite sides of the circumscribed quadrilateral is 10 cm, and its area is 12 cm2. Find the radius of the inscribed circle.

Answer 1

1.2 cm

Explanation:

Quadrilateral circumscribing a circle is a quadrangle whose sides are tangent to a circle inside it (see attached diagram).

The area of circumscribed quadrilateral is

`A=p\cdot r,`

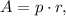
where
`p=(a+b+c+d)/(2)` is semi-perimeter and r is radius of inscribed circle.

In your case,
`A=12\ cm^2`

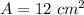
If a quadrilateral is circumscribed over the circle, then the sum of opposite sides is equal, so

`a+c=b+d=10\ cm,`

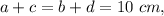
so

`P=10+10=20\ cm\\ \\p=(20)/(2)=10\ cm`

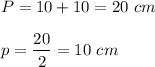
Now

`12=10\cdot r\Rightarrow r=(12)/(10)=1.2\ cm`