Question

Two cars simultaneously left Points A and B and headed towards each other, and met after 2 hours and 45 minutes. The distance between points A and B is 264 miles. What is the speeds of the cars, if one of the cars travels 14 mph faster than the other?

PLEASE ANSWER THANKS 20 POINTS

Answer 1

Hello!

The answers are:

`FirstCarSpeed=41mph\\SecondCarSpeed=55mph`

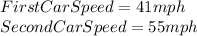
Why?

To calculate the speed of the cars, we need to write two equations in order to create a relation between the two speeds and be able to calculate one in function of the other.

So, let be the first car speed "x" and the second car speed "y", writing the equations we have:

For the first car:

`x_(FirstCar)=x_o+v*t`

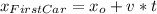
For the second car:

We know that the speed of the second car travels 14 mph faster than the first car, so:

`x_(SecondCar)=x_o+(v+14mph)*t`

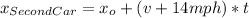
Now, we already know that both cars met after 2 hours and 45 minutes, and the distance between A and B is 264 miles, so, we can calculate the relative speed between both carsby the following way:

If the cars are moving towards each other the relative speed will be:

`RelativeSpeed=FirstCarSpeed-(-SecondCarspeed)\\\\RelativeSpeed=x-(-x-14mph)=2x+14mph`

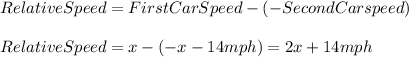
So , since we know that they covered a combined distance equal to 264 miles in 2 hours + 45 minutes, we have:

`2hours+45minutes=120minutes+45minutes=165minutes\\\\(165minutes*1hour)/(60minutes)=2.75hours`

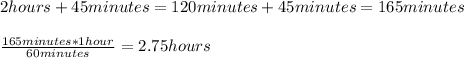
Writing the equation:

`264miles=(2x+14mph)*t\\\\264miles=(2x+14mph)*2.75hours\\\\2x+14mph=(264miles)/(2.75hours)\\\\2x=96mph-14mph\\\\x=(82mph)/(2)=41mph`

We have, the speed of the first car is equal to 41 mph.

Now, for the second car we have that:

`SecondCarSpeed=FirstCarSpeed+14mph\\\\SecondCarSpeed=41mph+14mph=55mph`

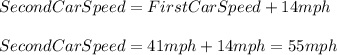
So, the speed of the second car is equal to 55 mph.

Hence, the answers are:

`FirstCarSpeed=41mph\\SecondCarSpeed=55mph`

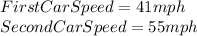
Have a nice day!