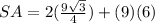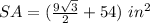Question

What is the total area of the prism?

Answer 1

The total area of the prism is
`SA=((9√(3))/(2)+54)\ in^(2)`

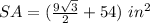
Explanation:

we know that

The surface area of the triangular prism of the figure is equal to

`SA=2B+PL`

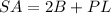
where

B is the area of the triangular face

P is the perimeter of the triangular face

L is the length of the prism

Find the area of the base B

The base is an equilateral triangle

so

Applying the law of sines the area is equal to

`B=(1)/(2)(3)^(2)sin(60\°)`

`B=(9√(3))/(4)\ in^(2)`

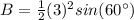
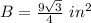
Find the perimeter P of the triangular face

`P=(3+3+3)=9\ in`

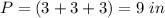
we have

`L=6\ in`

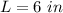
substitute

`SA=2((9√(3))/(4))+(9)(6)`

`SA=((9√(3))/(2)+54)\ in^(2)`