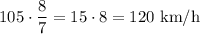Let
 be the speed of train A, and let's set the origin in the initial position of train A. The equations of motion are
be the speed of train A, and let's set the origin in the initial position of train A. The equations of motion are
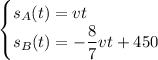
where
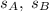 are the positions of trains A and B respectively, and t is the time in hours.
are the positions of trains A and B respectively, and t is the time in hours.
The two trains meet if and only if
 , and we know that this happens after two hours, i.e. at
, and we know that this happens after two hours, i.e. at

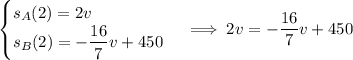
Solving this equation for v we have
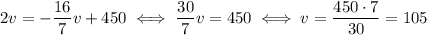
So, train A is travelling at 105 km/h. This implies that train B travels at