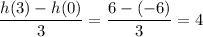Question

Drag each tile to the correct box. Consider the given functions f, g, and h.

h(x)=x²+x-6

Place the tiles in order from least to greatest according to the average rate of change of the functions over the interval [0, 3].

function H function f function g

Answer 1

g,f,h

I just took the test and was right

Explanation:

Answer 2

g, f, h

Explanation:

By definition, the average rate of change of a function f over an interval [a,b] is given by

`(f(b)-f(a))/(b-a)`

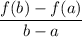
So, in your case, we want to compute the quantity

`(f(3)-f(0))/(3)`

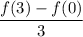
for all the three function

Average rate of change of f:

We will simply use the table to check the values for f(3) and f(0):

`(f(3)-f(0))/(3)=(10-1)/(3) = 3`

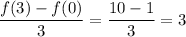
Average rate of change of g:

We will use the graph to to check the values for g(3) and g(0):

`(g(3)-g(0))/(3)=(8-1)/(3) = (7)/(3)`

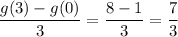
Average rate of change of h:

We can plug the values in the equation to get h(3) and h(0):

`h(3)=3^2+3-6=9+3-6=6,\quad h(0)=0^2+0-6=-6`

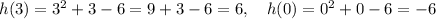
And so the average rate of change is

`(h(3)-h(0))/(3)=(6-(-6))/(3) = 4`