Answer:
The orbital period of the planet is 6.16 years.
Step-by-step explanation:
A planet has an average distance to the sun of 3.36 AU i.e. a = 3.36 AU
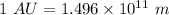
or
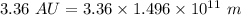
i.e. average distance,
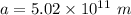
If we want to calculate the orbital period of the planet, it can be calculated using Kepler's third law as :
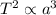

Where
M = mass of sun
G = universal gravitational constant
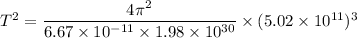
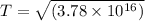
T = 194422220.952 seconds
Since,
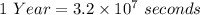
So, T = 194422220.952 seconds = 6.16 years
Hence, the orbital period of the planet is 6.16 years.