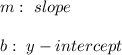Question

Which shows how to use similar right triangles to find the equation of the line...​

Answer 1

The first option would be the answer i believe

Explanation:

Answer 2

First Option

Explanation:

Triangles are are similar if we can turn one into the other by moving, rotating, flipping, or scaling. To solve this problem, we just need to match the ratios of the triangles. For both triangles we need to take the Change in y over the change in x, so:

`(change \ in \ y)/(Change \ in \x)=(y-b)/(x-0)=(m+b-b)/(1-0) \\ \\ y-b=mx \\ \\ \boxed{y=mx+b}`

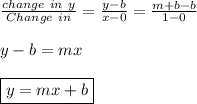
As you can see, this is the Slope-Intercept form of the equation of a line, where:

`m: \ slope \\ \\ b: \ y-intercept`