Question

D

=
number of dollars
p
=
number of pounds

Drag each table and equation to the unit rate it matches.

Answer 1

Answer: See image attached

Explanation:

Answer 2

General equation of line :
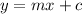`y = mx+c` --1

Where m is the slope or unit rate

Table 1)

p d

1 3

2 6

4 12

d = Number of dollars (i.e.y axis)

p = number of pound(i.e. x axis)

First find the slope

First calculate the slope of given points

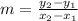`m = (y_2-y_1)/(x_2-x_1)` ---A

`(x_1,y_1)=(1,3)`

`(x_2,y_2)=(2,6)`

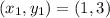
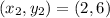
Substitute values in A

`m = (6-3)/(2-1)`

`m = 3`

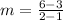
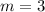
Thus the unit rate is 3 dollars per pound.

So, It matches the box 1 (Refer the attached figure)

Equation 1 :
`p=3d`

`(p)/(3)=d`

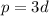
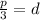
Since p is the x coordinate and d is the y coordinate

On Comparing with 1

`m = (1)/(3)`

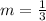
Thus the unit rate is
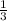`(1)/(3)` dollars per pound

So, It matches the box 2 (Refer the attached figure)

Equation 2 :
`(1)/(3)d=3p`

`d=9p`

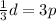
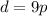
Since p is the x coordinate and d is the y coordinate

On Comparing with 1

`m =9`

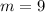
Thus the unit rate is 9 dollars per pound

So, It matches the box 3 (Refer the attached figure)

Table 2)

p d

1/9 1

1 9

2 18

d = Number of dollars (i.e.y axis)

p = number of pound(i.e. x axis)

`(x_1,y_1)=((1)/(9),1)`

`(x_2,y_2)=(1,9)`

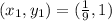
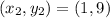
Substitute values in A

`m = (9-1)/(1-(1)/(9))`

`m = \frac{8}{frac{8}{9}}`

`m = 9`

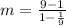
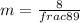
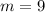
Thus the unit rate is 9 dollars per pound

So, It matches the box 3 (Refer the attached figure)