Question

Any help is appreciated please

Answer 1

C. It speeds up, and the angle increases

Step-by-step explanation:

We can answer by using the Snell's law:

`n_i sin \theta_i = n_r sin \theta_r`

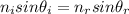
where

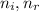`n_i, n_r` are the refractive index of the first and second medium

`\theta_i` is the angle of incidence (measured between the incident ray and the normal to the surface)

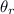`\theta_r` is the angle of refraction (measured between the refracted ray and the normal to the surface)

In this problem, light moves into a medium that has lower index of refraction, so

`n_r < n_i`

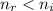
We can rewrite Snell's law as

`sin \theta_r =(n_i)/(n_r)sin \theta_i`

and since

`(n_i)/(n_r)>1`

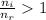
this means that

`sin \theta_r > sin \theta_i`

which implies

`\theta_r > \theta_i`

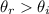
so, the angle increases.

Also, the speed of light in a medium is given by

`v=(c)/(n)`

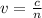
where c is the speed of light and v the refractive index: we see that the speed is inversely proportional to n, therefore the lower the index of refraction, the higher the speed. So, in this problem, the light will speed up, since it moves into a medium with lower index of refraction.