Question

Earth has a mass of 5.97 x 1024kg, and a mean radius of 6.38 x 10m. What would be the orbita

satellite in orbit 1.44 x 108 m above Earth?
a. v, = 630m/s,
c. v, - 1630m/s,
T = 2.78 x 10 s
T=5.78 x 10s
b. V = 1820m/s,
d. V, - 1260m/s,
T = 6.78 x 106 s
T=5.78 x 10's
Please select the best answer from the choices provid​

Answer 1

v = 1630 m/s

T = 5.78 x 10^5 s

Step-by-step explanation:

The tangential speed of the satellite can be found by requiring that the gravitational force on the satellite is equal to the centripetal force:

`G(Mm)/((R+h)^2)=m(v^2)/(R+h)`

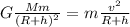
where

G is the gravitational constant

M=5.97 x 1024kg is the Earth's mass

m is the satellite's mass

`R=6.38 \cdot 10^6 m` is the Earth's radius

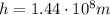`h=1.44\cdot 10^8 m` is the altitude of the satellite

v is the speed of the satellite

Solving for v,

`v=\sqrt{(GM)/(R+h)}=\sqrt{((6.67\cdot 10^(-11))(5.97\cdot 10^(24)kg))/(6.38\cdot 10^6 m+1.44\cdot 10^8 m)}=1627 m/s \sim 1630 m/s`

And the period of the orbit is equal to the ratio between the distance covered during one revolution (the circumference of the orbit) and the speed:

`T=(2 \pi (R+h))/(v)=(2\pi (6.38\cdot 10^6 m+1.44\cdot 10^8 m))/(1630 m/s)=5.79\cdot 10^5 s`

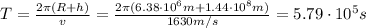
So the correct answer is

v = 1630 m/s

T = 5.78 x 10^5 s