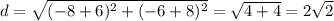Question

Please Help Its Urgent

A bridge crosses a circular lake. The bridge is represented by the function y −x = 2 and the lake is represented by the function x^2 +y ^2 = 100.

a. What is the radius of the lake?

b. Find the length of the bridge.

Answer 1

We can rewrite the equation of the circle as

`(x-0)^2+(y-0)^2=10^2`

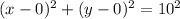
so that we can be in the form

`(x-h)^2+(y-k)^2=r^2`

When you write the equation of a circle in this form, then the center is
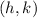`(h,k)` and the radius is
`r`.

So, in our case, the radius of the circle is 10.

To find the length of the bridge, we find the two points where the bridge crosses the lake (i.e. we solve the system between the equations of the line and the circle), and compute the distance between those points:

`\begin{cases}y=x+2\\x^2+y^2=100\end{cases}\implies\begin{cases}y=x+2\\x^2+(x+2)^2=100\end{cases}`

Solving the second equation for x, we have

`x^2+(x+2)^2=100 \iff x^2+x^2+4x+4=100\iff\\2x^2+4x-96=0 \iff x^2+2x-48=0\\\iff x=-8\ \lor\ x=6`

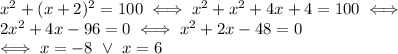
We use the first equation to compute the correspondent values of y:

`x=-8\implies y=x+2=-6 \implies P_1 = (-8,-6)`

`x=6\implies y=x+2=8 \implies P_1 = (6,8)`

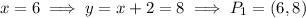
Now, the distance between these two points is given by the pythagorean's theorem:

`d = √((-8+6)^2+(-6+8)^2) = √(4+4)=2√(2)`