Question

What is the sum of the infinite geometric series?

Answer 1

-288

Explanation:

n=1/2 divided by -144. You then just plug that number which is .00347 into n in the equation and use a scientific calculator to find the answer.

Answer 2

The sum of the infinite geometric series is:

-288

Explanation:

We know that the sum of the infinite geometric series:

`\sum_(n=1)^(\infty) ar^(n-1)`

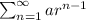
is given by the formula:

`Sum=(a)/(1-r)`

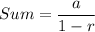
The series is given by:

`\sum_(n=1)^(\infty) (-144)\cdot ((1)/(2))^(n-1)`

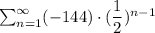
By looking at the series we observe that the first term of the series is:

`a=-144`

and the common ratio of the series is:

`r=(1)/(2)`

Hence, the sum of the series is:

`Sum=(-144)/(1-(1)/(2))\\\\Sum=(-144)/((1)/(2))\\\\Sum=-144* 2\\\\Sum=-288`