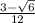Answer:
see explanation
Explanation:
The area of the shaded triangle = area of ΔABD - area of ΔADC
A of ΔABD =
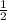 × AD × BD
× AD × BD
A =
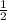 ×
×
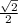 ×
×
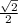
=
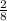 =
=
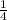
--------------------------------------------------------------------------
A of ΔACD =
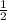 × AD × DC
× AD × DC
A =
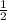 ×
×
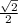 ×
×
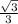
A =
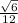
-------------------------------------------------------------------------
shaded area =
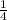 -
-
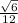
=
 -
-
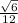 =
=