Answer:
The volume of the figure is
![((l^(3))/(3))[(\pi )/(2)-1]\ units^(3)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/n7twtxqgz9bopo9ps89a9upplzdxk0eubs.png)
Explanation:
we know that
The volume of the figure is equal to the volume of the cone minus the volume of the square pyramid
step 1
Find the volume of the cone
The volume of the cone is equal to
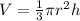
we have
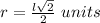 ----> the diagonal of the square base of pyramid is equal to the diameter of the cone
----> the diagonal of the square base of pyramid is equal to the diameter of the cone

substitute
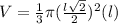
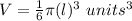
step 2
Find the volume of the square pyramid
The volume of the pyramid is equal to

where
B is the area of the base
h is the height of the pyramid
we have

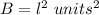
substitute
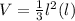
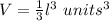
step 3
Find the volume of the figure
![(1)/(6)\pi (l)^(3)\ units^(3)-(1)/(3)l^(3)\ units^(3)=((l^(3))/(3))[(\pi )/(2)-1]\ units^(3)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/yz06d9opxhah4jad391tovnhfnohxoxxx3.png)