Question

Precalculus Homework help please.

Answer 1

see explanation

Explanation:

(5)

Using the trigonometric identity

sin²x + cos²x = 1 ⇒ cos²x = 1 - sin²x

Given

3sin²Θ + 2cos²Θ - 2

= 3sin²Θ + 2(1 - sin²Θ) - 2

= 3sin²Θ + 2 - 2sin²Θ - 2

= sin²Θ

(6)

Using the trigonometric identity

secx =
`(1)/(cosx)`

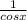
Consider the left side

`(cosx)/(1-sin^2x)`

=
`(cosx)/(cos^2x)`

=
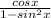
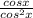
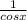`(1)/(cosx)` = secx = right side ⇒ verified

(7)

Using the trigonometric identity

1 + cot²x = csc²x

Given

sin²x. cot²x + sin²x ← factor out sin²x from each term

= sin²x(cot²x + 1)

= sin²x. csc²x

= sin²x ×
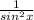`(1)/(sin^2x)` = 1