Question

According to the general equation for conditional probability, if (image attached)

A. 2/3
B. 1/3
C. 1/6
D/ 5/6

Answer 1

The correct answer option is B. 1/3.

Explanation:

We are given that P (A ∩ B') = 2/9 and P (B') = 1/3 and we are to find P (A | B').

We also know that the formula of conditional probability is given by:

P (A | B') = P (A ∩ B') / P (B)

So substituting the given values in the formula above to get the value of P (A | B'):

P (A | B') =
`\frac { \frac { 2 } { 9 } } { \frac { 1 } { 3 } } = \frac { 2 } { 9 } * \frac { 3 } { 1 }` = 1/3

Answer 2

Option B

`P(A|B') = (1)/(3)`

Explanation:

If B 'is the complement of B then
`P(B') = P({\displaystyle {\overline {B}}})=1-P(B) = (2)/(3)`

In a probabilistic experiment, when two events A and B are dependent on each other, then the probability of occurrence A since B occurs is:

`P(A|B') = (P(A\ and\ B))/(P(B'))`

Then if
`P(A\ and\ B) = (2)/(9)` and
`P(B') = (2)/(3)`

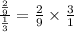`P(A|B') = ((2)/(9))/((2)/(3))\\\\P(A|B') = (1)/(3)`