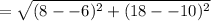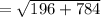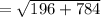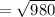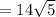Question

Please help its due tonight.

A bridge crosses a circular lake. The bridge is represented by the function

y −x = 2 and the lake is represented by the function x^2 +y ^2 = 100.

a. What is the radius of the lake?

b. Find the length of the bridge.

Answer 1

a) The radius of the lake to be r=10 units.

b)
`14√(5)` units

Explanation:

The lake has equation:
`x^2+y^2=100`

We can rewrite this as
`x^2+y^2=10^2`

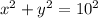
Comparing this to
`x^2+y^2=r^2`

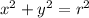
We have the radius of the lake to be r=10 units.

b) The bridge is represented by the function y −x = 2

This is the same as y=x+2

We substitute this into the equation of the circle to get:

`x^2+(x+2)^2=100`

`x^2+x^2+4x+4-100=0`

`2x^2+4x-96=0`

`x^2+2x-48=0`

`(x+8)(x-6)=0`

`x=-8,x=6`

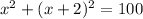
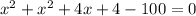
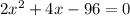
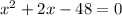
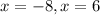
When x=8, y=2(8)+2=18

When x=-6, y=2(-6)+2=-10

The length of the bridge is the distance between the points (8,18) and (-6,-10)

`=√((8--6)^2+(18--10)^2)`

`=√(196+784)`

`=√(196+784)`

`=√(980)`

`=14√(5)`