Answer:
The correct option is 3.
Explanation:
The volume of a square pyramid is
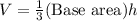
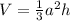 .... (1)
.... (1)
Where, a is th side of base and h is the height of pyramid.
From the given figure it is clear that the height of the pyramid is 10 cm and the length of base is 12 cm.
Substitute a=12 and h=10 in equation (1), to find the volume of the square pyramid.
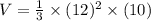
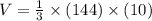
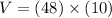
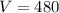
The volume of pyramid is 480 cm³. Therefore the correct option is 3.