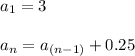Answer:
The explicit formula
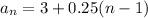
The recursive formula
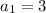 for
for
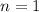
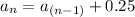 if
if
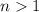
Explanation:
If a sequence is arithmetical then the difference between any of its consecutive terms will be constant
3, 3.25, 3.5, 3.75,
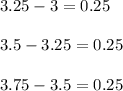
The difference between the consecutive terms remains constant so the sequence is arithmetic.
The explicit formula for an arithmetic sequence is:
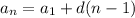
Where d is the constant difference between the terms.
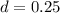
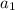 is the first term of the sequence.
is the first term of the sequence.
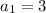
So
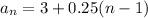
Finally, the recursive formula is: