Question

If a 25.0 ml sample of sulfuric acid is titrated with 50.0 ml of 0.200 M potassium hydroxide to a phenolphthalein endpoint, what is the molarity of the acid?

A) 0.150 M
B) 0.100 M
C) 0.200 M
D) 0.300 M
E) 0.400 M

Answer 1

Molarity of the sulfuric acid is Choice C): 0.200 M.

Step-by-step explanation:

The unit for molarity "M" stands for moles per liter. Convert all volume to liters:

• 
  `V({\rm NaOH}) = \rm 50.0\;ml = 50.0* 10^(-3)\;L = 5.00* 10^(-2)\;L`;
• 
  `V({\rm H_2SO_4}) = \rm 25.0\;ml = 25.0* 10^(-3)\;L = 2.50* 10^(-2)\;L`.

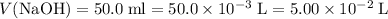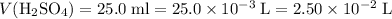How many moles of potassium hydroxide is required to reach the equivalence endpoint?

`n({\rm NaOH}) = c \cdot V = 0.200\;\text{mol}\cdot\text{L}^(-1) * 5.00times 10^(-2) \;\text{L} = 1.00* 10^(-2)\;\text{mol}`.

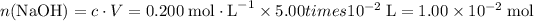How many moles of sulfuric acid in the original solution?

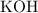`\rm KOH` neutralizes
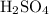`\rm H_2SO_4` at a two-to-one ratio:

`\rm 2\;KOH\;(aq) +H_2SO_4\;(aq) \to K_2SO_4\;(aq) + H_2O\;(l)`.

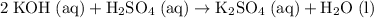The
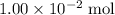`1.00* 10^(-2)\;\text{mol}` moles of
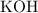`\rm KOH` will neutralize only half as much
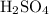`\rm H_2SO_4`. That is:

`\displaystyle n({\rm H_2SO_4}) = \rm (1)/(2)* (1.00* 10^(-2)\;mol)= 5.00* 10^(-3)\;mol`.

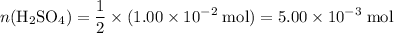What's the molarity of the
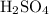`\rm H_2SO_4` solution?

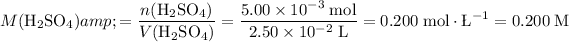`\displaystyle \begin{aligned}M({\rm H_2SO_4}) &= \frac{n(\rm H_2SO_4)}{V({\rm H_2SO_4})}=\rm (5.00* 10^(-3)\;mol)/(2.50* 10^(-2)\;L) = 0.200\;mol\cdot\L^(-1) = 0.200\;M\end{aligned}`.