Answer: The dimensions of the field are
width = 40 ft and length = 60 ft.
Step-by-step explanation: Given that a field with an area of 2880 ft² has the shape of a rectangle with length 12 ft larger than the width.
We are to find the dimensions of the field.
Let w ft be the width of the given rectangular field.
Then, the length of the field will be (w + 12) ft.
According to the given information, we have
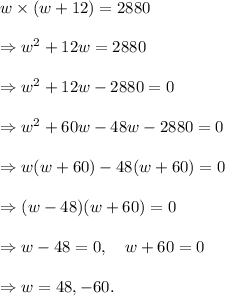
Since the measure of a side of a rectangle cannot be negative, so w = 48.
This implies that
length of the field = w + 12 = 48 + 12 = 60 ft.
Thus, the dimensions of the field are
width = 40 ft and length = 60 ft.