Question

What is the equation of the line that passes through (4,-1) and (-2,3)

Answer 1

2x+3y-5=0

Explanation:

We have been given two points (4,-1) and (-2,3). Now we need to find about

what is the equation of the line that passes through (4,-1) and (-2,3).

Slope of the line through the points (4,-1) and (-2,3) is given by:

`m=(y_2-y_1)/(x_2-x_1)`

`m=(3-\left(-1\right))/(-2-4)=(3+1)/(-6)=(4)/(-6)=-(2)/(3)`

Now plug the slope
`m=-(2)/(3)` and point (4,-1) into point slope formula

`y-y_1=m\left(x-x_1\right)`

`y--1=-(2)/(3)\left(x-4\right)`

`y=-(2)/(3)x+(5)/(3)`

or we can rewrite that as 2x+3y-5=0

Hence final answer is 2x+3y-5=0

Answer 2

Hello!

The answer is:

The second option

`2x+3y-5=0`

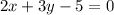
Why?

To know which is the equation of the line, we need to follow the next steps:

Find the slope of the line:

We are given the points:

`(-2,3)\\(4,1)`

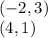
Where,

`x_1=4\\y_1=-1\\x_2=-2\\y_2=3`

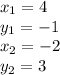
Also, we know that we can calculate the slope of a function using the following formula:

`m=(y_2-y_1)/(x_2-x_1)`

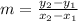
Now, using the slope formula, and substituting the given points, we have:

`m=(3-(-1))/(-2-4)`

`m=(4)/(-6)`

`m=-(2)/(3)`

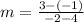
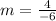
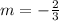
Find the "b" value:

In order to find "b" we need to substitute any of the given points, we know that line pass through both of the given points, so, substituting the point (4,-1), we have:

Writing the slope form of the function,

`y=mx+b`

`y=-(2)/(3)x+b`

`-1=-(2)/(3)*(4)+b\\\\b=-1+(2)/(3)*(4)=-1+(8)/(3)=(-3+8)/(3)=(5)/(3)`

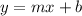
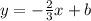
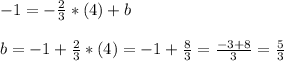
Now that we know the slope and "b", we can write the equation of the line in slope-intercept form:

Writing the equation of the equation, we have:

`y=-(2)/(3)x+(5)/(3)`

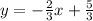
Then, by multiplying each side of the equation by 3 in order to simplify the fractions, we have:

`3y=(3)*(-(2)/(3)x)+(3)*((5)/(3))`

`3y=-2x+5`

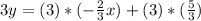
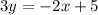
Rewriting the equation, we have:

`2x+3y-5=0`

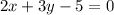
Hence, we have that the correct option is the second option, the equation of the line that passes through the given points is:

`2x+3y-5=0`

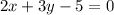
Have a nice day!