Question

Find any 3 (x,y) pairs that are solutions for the equation 2x-5y=10 . Show your work

Answer 1

Hello!

The answers is:

The three points that are solution for the equation are:

`(5,0)\\(0,-2)\\(6,0.4)`

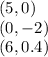
Why?

To find 3 pairs (x,y) or points that are solutions for the equation, we could find where the function intercepts the x-axis and y-axis, we must remember that the domain of a line is all the real numbers, so by using any input, we will find a solution, which means finding a point that belongs to the line.

So,

Finding the axis intercepts of the line, we have:

x-axis intercept:

Making "y" equal to 0, we have:

`2x-5y=10`

`2x-5*(0)=10`

`2x=10`

`x=(10)/(2)=5`

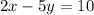
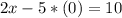
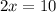
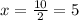
We have that the interception point with the x-axis is (5,0)

y-axis intercept:

Making "x" equal to 0, we have:

`2x-5y=10`

`2*(0)-5y=10`

`0-5y=10`

`5y=-10`

`y=(-10)/(5)=-2`

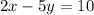
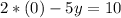
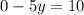
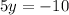
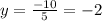
We have that the interception point with the y-axis is (0,-2)

As we know, the domain of a line is equal to the real numbers, Now, we have that any between the points (5,0) and (0,-2) will belong to the line, so, let's try with a point wich x-coordinate (input) is equal to 6 and then find the y-coordinate (output) if the point satisfies the equality, it belongs to the equation to the line.

Substituting x equal to 6, we have:

`2*(6)-5y=10`

`12-5y=10`

`12-10=5y`

`y=(12-10)/(5)=(2)/(5)`

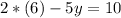
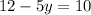
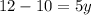
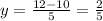
So, the obtained point is:

`(6,(2)/(5))`

or

`(6,0.4)`

Now, let's prove that it belongs to the equation of the line by substituting it into the equation:

`2*(6)-5*(2)/(5)=10`

`12-2=10`

`10=10`

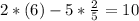
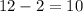
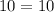
We can see that the equality is satisfied, it means that the point belongs to the line.

Hence, the three points that are solutions for the equation are:

`(5,0)\\(0,-2)\\(6,0.4)`

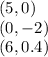
Have a nice day!

Answer 2

(0,-2), (5,0) and (10,2).

Explanation:

Given equation is
`2x-5y=10`.

Now we need to find 3 pairs of solutions in (x,y) form for the given equation.

As
`2x-5y=10` is a linear equation so we are free to pick any number for x like x=0, 5, 10

Plug x=0 into
`2x-5y=10`, we get:

`2(0)-5y=10`

`0-5y=10`

`-5y=10`

`y=(10)/(-5)`

`y=-2`

Hence first solution is (0,-2)

We can repeat same process with x=5 and 10 to get the other solutions.

Hence final answer is (0,-2), (5,0) and (10,2).