Question

A line passes through the points (2,4) and (-4,-1). Find its equation in slope-intercept form. (2 points, 1 for work, 1 for equation)

Answer 1

Hello!

The answer is:

The equation of the line in slope-intercept form:

`y=(5)/(6)x+(7)/(3)`

Why?

To find the equation in slope-intercept form, we need to follow the next steps:

Find the slope of the line:

Using the slope formula, we have:

`m=(y_2-y_1)/(x_2-x_1)`

We are given the points:

`(2,4)\\(-4,-1)`

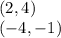
So, substituting we have:

`m=((-1)-(4))/(-4-2)`

`m=(-5)/(-6)`

`m=(5)/(6)`

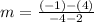
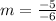
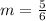
Find the "b" value:

Now that we know the value of the slope, we can write the equation of the line:

`y=(5)/(6)x+b`

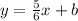
In order to find "b" we need to substituite any of the given points, we know that line is thru both of the given points, so, substituting (2,4) we have:

`4=(5)/(6)*2+b\\\\4=(10)/(6)+b\\\\4=(5)/(3)+b\\\\b=4-(5)/(3)=\frac{(3*4)-5}3}=(12-5)/(3)=(7)/(3)`

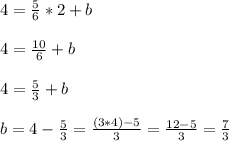
Now that we know the slope and "b", we can write the equation of the line in slope-intercept form:

`y=(5)/(6)x+(7)/(3)`

Have a nice day!