10) What is the base of the triangle?
From this triangle we know:
THE AREA:
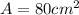
THE HEIGHT:
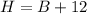
We know that the area, height, and base of a triangle are related according to the following formula:
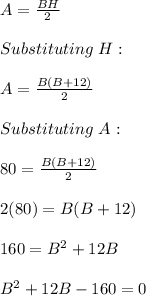
Solving B by quadratic formula:
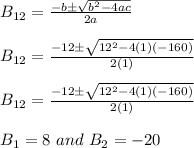
Since we can’t have a negative value of the base, the correct option is:
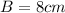
11) How long will it take the water balloon to hit the ground?
We must use the formula:

Since James drops the balloon from a height of 45m, then this is the initial height, so
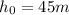 . Moreover, at the very instant he drops the balloon the initial velocity is zero, so
. Moreover, at the very instant he drops the balloon the initial velocity is zero, so
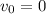 . When the ballon hit the ground
. When the ballon hit the ground
 . Therefore:
. Therefore:
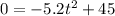
Solving this equation:
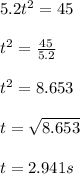
Rounding to the nearest tenth:
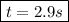
Finally, the water balloon will hit the ground after 2.9 seconds.
12) Height and initial velocity
We have the equation:

But we know that this equation follows the form:
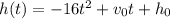
According to this:
The height of the platform is
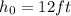
The initial velocity of the ball is
