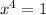Answer:
The substitution is
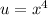
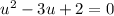
Explanation:
We have the 8th degree polynomial equation
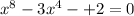
To rewrite the equation as a quadratic function, take the common factor of the term x with the smallest exponent, in this case it is
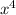 .
.
Now make a change of variable
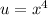 .
.
So rewriting the equation in terms of u, we have:
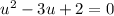
Now the initial equation became a quadratic equation
Factoring is left:
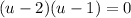
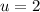 and
and
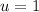
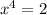 and
and