Question

Please answer photo below thank you :’)

Answer 1

Answer:x2_>16 B.

Explanation:

Answer 2

For this case we will show that the correct option is option C.

`x ^ 2 \leq16`

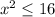
We find the value of the variable "x":

We apply root to both sides of the equation to eliminate the exponent:

`x \leq \pm \sqrt {16}\\x \leq \pm4`

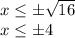
We found the first solution with the positive value:

`x \leq4`

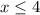
We use the negative value to find the other solution. Since it is an inequality, the sign of the inequality changes in the negative portion of the solution.

`x \geq-4`

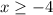
So, the roots are:

`x_ {1} \geq-4\\x_ {2} \leq + 4`

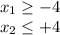
The solution is given by the values of "x" greater than or equal to -4 and less than or equal to 4

Answer:

Option C