Question

Which equation matches the function shown in the graph? A) y = x + 4 B) y = 4x + 2 C) y = 2x + 4 D) y = -2x + 4

Answer 1

Slope-intercept form: y = mx + b (m is the slope, b is the y-intercept or the y value when x = 0 --> (0 , y))

To find the slope(m), you can use the slope formula, then you can find and plug in 2 points into the equation

`m=(y_2-y_1)/(x_2-x_1)` (x₁ , y₁) is the first point you have on the left, (x₂ , y₂) is the point to the right of the first point

You can also find the slope by:

`m=(rise)/(run)`

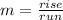
"rise" is the number of units you go up (positive number) or down (negative number), and "run" is the number of units you go to the right. For example if your slope is -2, you go down 2 units and to the right 1 unit.

So you can just look at the graph and see how many units a point goes up/down and to the right to get to the next point

To find the y-intercept, find the point where the line crosses through the y-axis, or (0, y)

Answer 2

The equation that matches the function shown in the graph is y = 2x + 4

Which equation matches the function shown in the graph?

From the question, we have the following parameters that can be used in our computation:

The graph

A linear equation is represented as

y = mx + c

Where

m = slope

c = y-intercept

From the graph, we have the point (0, 4)

This means that

c = 4

So, we have

y = mx + 4

Using the point (-2, 0) on the graph, we have

-2m + 4 = 0

This gives

2m = 4

m = 2

Recall that

y = mx + 4

So, we have

y = 2x + 4

Hence. the equation is y = 2x + 4