Question

10 POINTS PLEASE HELP!

Answer 1

When the surrounding flaps are folded up, the base of the box will have dimensions
`11-2x` by
`16-2x`, and the box will have a height of
`x`. So the box has volume, as a function of
`x`,

`V(x)=(11-2x)(16-2x)x=176x-54x^2+4x^3`

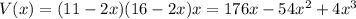
I don't know what technology is available to you, but we can determine an exact value for
`x` that maximizes the volume by using calculus.

Differentiating
`V` with respect to
`x` gives

`(\mathrm dV)/(\mathrm dx)=176-108x+12x^2`

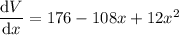
and setting this equal to 0 gives two critical points at

`x=\frac{27\pm√(201)}6\implies x\approx2.1\text{ or }x\approx6.9`

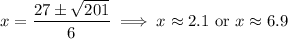
For the larger critical point we would get a negative volume, so we ignore that one. Then the largest volume would be about 168.5 cubic in.