Answer:
Values of x are 4i, -4i, 5 and -5
Explanation:
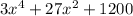 We need to find all the zeros (roots) of the above equation.
We need to find all the zeros (roots) of the above equation.
Let assume that x^4 = u^2 and x^2 = u
Putting values of x^4 and x^2 in the above equation and finding the value of u.
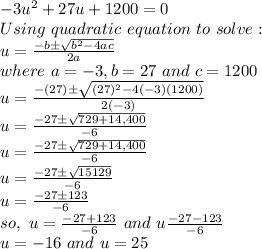
So, values of u are -16 and 25
Putting back the value of u i.e, x^2
x^2 = -16 and x^2 =25
solving
Taking square root on both sides:
√x^2 =√-16 and √x^2 = √25
x = ± 4i (as √-1 =i) and x = ±5
So, values of x are 4i, -4i, 5 and -5.