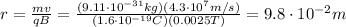Question

An electron in a cathode-ray beam passes between 2.5-cm-long parallel-plate electrodes that are 5.6 mm apart. A 2.5 mT , 2.5-cm-wide magnetic field is perpendicular to the electric field between the plates. The electron passes through the electrodes without being deflected if the potential difference between the plates is 600 V . Part A What is the electron's speed? Express your answer to two significant figures and include the appropriate units. v v = nothingnothing SubmitRequest Answer Part B If the potential difference between the plates is set to zero, what is the electron's radius of curvature in the magnetic field? Express your answer to two significant figures and include the appropriate units. r r = nothingnothing

Answer 1

A)
`4.3\cdot 10^7 m/s`

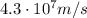
For an electron moving in a region with both electric and magnetic field, the electron will move undeflected if the electric force on the electron is equal to the magnetic force:

`qE= qvB`

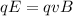
which means that the speed of the electron will be

`v=(E)/(B)`

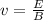
where

E is the magnitude of the electric field

B is the magnitude of the magnetic field

In this problem,

`B=2.5 mT=0.0025 T` is the intensity of the magnetic field

The electric field can be found as

`E=(V)/(d)`

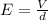
where

V = 600 V is the potential difference between the electrodes

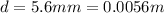`d=5.6 mm=0.0056 m` is the distance between the electrodes

Substituting,

`E=(600 V)/(0.0056 m)=1.07\cdot 10^5 V/m`

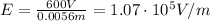
So the electron's speed is

`v=(1.07\cdot 10^5 V/m)/(0.0025 T)=4.3\cdot 10^7 m/s`

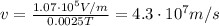
B)
`9.8\cdot 10^(-2) m`

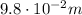
The radius of curvature of an electron in a magnetic field can be found by equalizing the centripetal force to the magnetic force:

`m(v^2)/(r)=qvB`

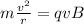
where

m is the electron mass

v is the speed

r is the radius of curvature

q is the charge of the electron

Solving for r, we find

`r=(mv)/(qB)=((9.11\cdot 10^(-31) kg)(4.3\cdot 10^7 m/s))/((1.6\cdot 10^(-19) C)(0.0025 T))=9.8\cdot 10^(-2) m`