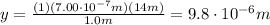Question

At sunset, red light travels horizontally through the doorway in the western wall of your beach cabin, and you observe the light on the eastern wall. Assume that the light has a wavelength of 700 nm, that the door is 1.0 m wide, and that the distance from the door to the far wall of your cabin in 14 m .Part ADetermine the distance between the central bright fringe and a first-order dark fringe of the interference pattern created by the doorway "slit".

Answer 1

`9.8\cdot 10^(-6)m`

Step-by-step explanation:

For light passing through a single slit, the position of the nth-minimum from the central bright fringe in the diffraction pattern is given by

`y=(n \lambda D)/(d)`

where

`\lambda` is the wavelength

D is the distance of the screen from the slit

d is the width of the slit

In this problem, we have

`\lambda=700 nm = 7.00\cdot 10^(-7)m` is the wavelength of the red light

D = 14 m is the distance of the screen from the doorway

d = 1.0 m is the width of the doorway

Substituting n=1 into the equation, we find the distance between the central bright fringe and the first-order dark fringe (the first minimum):

`y=((1)(7.00\cdot 10^(-7) m)(14 m))/(1.0 m)=9.8\cdot 10^(-6)m`