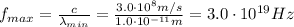(a)

The frequency of an electromagnetic wave is given by
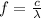
where
c is the speed of light
 is the wavelength
is the wavelength
We notice from the formula that the frequency is inversely proportional to the wavelength, so the minimum frequency corresponds to the maximum wavelength, and viceversa
The maximum value of the wavelength of the visible light waves is
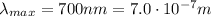 (red light)
(red light)
so the minimum frequency of visible light is
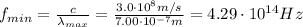
(b)
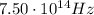
The maximum frequency corresponds to the minimum wavelength;
The minimum wavelength is
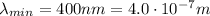 (violet light)
(violet light)
so the maximum frequency of visible light is
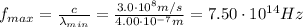
(c) 1 m
The wavelength of an electromagnetic wave is given by
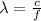
as before, we notice that the minimum wavelength corresponds to the maximum frequency, and viceversa.
The maximum frequency of shortwave radio waves is
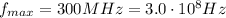
so the minimum wavelength of these waves is
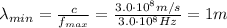
(d) 200 m
The minimum frequency of shortwave radio waves is

so the maximum wavelength of these waves is
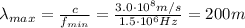
(e)
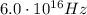
As in part (a) and (b), we can find the frequency of the X-rays by using the formula
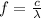
The maximum wavelength of the x-rays is
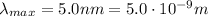
so the minimum frequency is
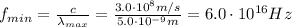
(f)
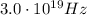
The maximum frequency corresponds to the minimum wavelength;
The minimum wavelength is

so the maximum frequency of the x-rays is