Question

Please answer right away

Answer 1

The correct answer option is 6.13.

Explanation:

We are given a scalene triangle which has no equal side and we are to find the unknown side length x.

Since the total measure of angles of a triangle is 180°, so we can find the measure of the unknown angle.

180° - 70° + 60° = 50°

Now we can use the sine formula to find the value of x.

`(x)/(sin70) =(5)/(sin50)`

`x=(5)/(sin50) * sin70`

`x=6.13`

Answer 2

6.13

Explanation:

Using Sine Law we know that

`(a)/(SinA)=(b)/(SinB)=(c)/(SinC)`

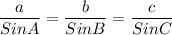
Using your figure let's assign sides and angles:

A=? B = 60° C = 70°

a = 5 b = ? c = x

If we put that into our formula:

`(5)/(Sin?)=(?)/(Sin60)=(x)/(Sin70)`

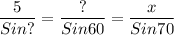
Notice that we have too many unknowns. We need to complete at least one ratio to do this, so how do we do this?

Notice we have 2 angles given, so we solve for the third angle. The sum of all angles in any triangle is always 180°

∠A + ∠B + ∠C= 180°

∠A + 60° + 70° = 180°

∠A + 130° = 180°

∠A = 180° - 130°

∠A = 50°

Now we can use this to solve for x.

`(5)/(Sin50)=(x)/(Sin70)\\\\((5)(Sin70))/(Sin50) = x\\\\(4.6985)/(0.7660)=x\\\\6.1338 =x`

So the closest answer would be 6.13