Answer: B. Can be used to derive Kepler's third law of planetary motion.
Step-by-step explanation:
According to Newton's law of universal gravitation:
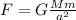 (1)
(1)
Where:
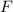 is the module of the force exerted between both bodies
is the module of the force exerted between both bodies
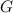 is the universal gravitation constant.
is the universal gravitation constant.
 and
and
 are the masses of both bodies.
are the masses of both bodies.
 is the distance between both bodies
is the distance between both bodies
If we apply this law for two bodies in a circular orbit:
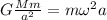 (2)
(2)
Where:
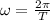 is the angular velocity, which is related to the period of the orbit
is the angular velocity, which is related to the period of the orbit

Substituting
 in (2):
in (2):
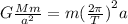 (3)
(3)
Finding
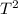 :
:
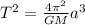 (4)
(4)
Knowing
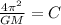 is a constant:
is a constant:
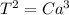
We finally get to 3rd Kepler's law of planetary motion:
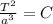 (5)
(5)