Question

The number of people playing a new phone app game triples every month. When the app first launched, 800 people started playing the game right away. There are currently 194,400 people playing the game. Write an equation to represent this situation, and determine the number of months, t, that have passed since the app launched.

Answer 1

800(3)^t = 194,400; t = 5 months

Explanation:

Answer 2

`a_t=ar^(t-1)`

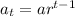
t=6 months

Explanation:

We are given that the number of people playing a new phone app game triples every month

When the app first launch , the number of people started playing the game right away=800

According to question

The number of peoples are currently playing the game=194,400

We solve by using the formula of geometric series because we get a geometric series pattern

The number of people playing the game when app game launch=800

The number of people playing game after one month=2400

800,2400,7200,........,194,400

`a_1=800,a_2=2400,a_3=7200,a_t=194,400`

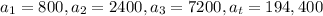
We are finding common ratio

`(a_2)/(a_1)=(2400)/(800)=3`

`(a_3)/(a_2)=(7200)/(2400)=3`

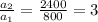
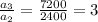
Hence, the common ratio is 3 therefor nth term of G.P

`a_t=ar^(t-1)`

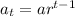
a=800,r=3,
`a_t=194,400`

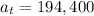
Substitute the values then we get

`194,400=800(3)^(t-1)`

`\frac[194400}{800}=(3)^(t-1)`

`243=3^(t-1)`

`3^5=3^(t-1)`

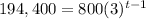
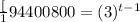
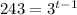
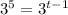
When base are same on both side then the power are equals

Therefore, t-1=5

t=5+1=6

Hence, when there are 194,400 people currently playing the game then

the number of months ,t=6 that have passed since the app launched.