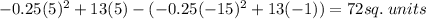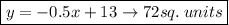Match each curve to the area under it on the interval [-1, 5]. y = x2 + 16 42 square units y = -x2 + 7x 72 square units y = 4x + 26 204 square units y = -0.5x + 13 138 square units - QAmmunity.org

Match each curve to the area under it on the interval [-1, 5]. y = x2 + 16 42 square units y = -x2 + 7x 72 square units y = 4x + 26 204 square units y = -0.5x + 13 138 square units

asked Dec 22, 2020 39.7k views

2 Answers

Answer:

1.
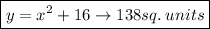
$\boxed{y=x^2+16\to138sq.\:units}$

2.
$\boxed{y=-x^2+7x\to42sq. \:units}$

3.
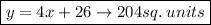
$\boxed{y=4x+26\to 204sq.\:units}$

4.
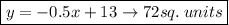
$\boxed{y=-0.5x+13\to72sq.\:units}$

Explanation:

1. The first curve is
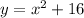
y=x^2+16

The area under this curve on the interval [-1, 5] is given by:

$\int\limits^5_(-1) {x^2+16} \, dx$

We integrate to obtain:

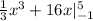
(1)/(3)x^3+16x|_(-1)^5

We evaluate to obtain:

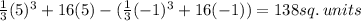
$(1)/(3)(5)^3+16(5)-((1)/(3)(-1)^3+16(-1))=138sq.\:units$

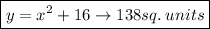
$\boxed{y=x^2+16\to138sq.\:units}$

2. The second curve is
y=-x^2+7x .

The area under this curve on the interval [-1, 5] is given by:

$\int\limits^5_(-1) {-x^2+7x} \, dx$

We integrate this function to obtain:

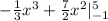
-(1)/(3)x^3+(7)/(2)x^2|_(-1)^5

This evaluates to

-(1)/(3)(5)^3+(7)/(2)(5)^2-(-(1)/(3)(-1)^3+(7)/(2)(-1)^2)=42 square units.

$\boxed{y=-x^2+7x\to42sq. \:units}$

3. The third curve is
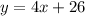
y=4x+26

The area under this curve on the interval [-1, 5] is given by:

$\int\limits^5_(-1) {4x+26} \, dx$

We integrate this function to obtain:

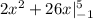
2x^2+26x|_(-1)^5

We evaluate the limits of integration to obtain:

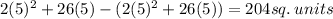
$2(5)^2+26(5)-(2(5)^2+26(5))=204sq.\:units$

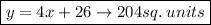
$\boxed{y=4x+26\to 204sq.\:units}$

4. The fourth curve is
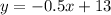
y=-0.5x+13

The area under this curve on the interval [-1, 5] is given by:

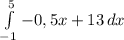
$\int\limits^5_(-1) {-0,5x+13} \, dx$

We integrate this function to obtain:

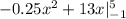
-0.25x^2+13x|_(-1)^5

We evaluate the limits of integration to obtain:

$-0.25(5)^2+13(5)-(-0.25(-15)^2+13(-1))=72sq.\:units$

$\boxed{y=-0.5x+13\to72sq.\:units}$

IcedDante answered Dec 28, 2020

4.6k points

Search QAmmunity.org