Answer:
if it has two real repeated solutions then t=-9/8
if it has two real distinct solutions then t>-9/28
Explanation:
Given:
tx^2+3x-7=0
Also above equation has two real solutions
Now what can deduced about the value of t?
For any quadratic equation "ax^2 +bx +c=0" the solution is given by the quadratic formula
x=
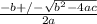
The part under the square root i.e b^2 - 4ac is called the discriminant and it decides whether the equation will have 1 solution, 2 solution or no solution.
if discriminant is negative, i.e. <0 then equation will have no real solution
if discriminant is zero, i.e. =0 then equation will have two repeated real solution
if discriminant is positive, i.e >0 then equation will have two real distinct solution
As given equation has two real solutions:
if they are distinct then
b^2-4ac>0
Putting values of a=t, b=3, c=-7 in above we get,
9+28t>0
28t>-9
t>-9/28
if they are repeated then
b^2-4ac=0
Putting values of a=t, b=3, c=-7 in above we get,
9+28t=0
28t=-9
t=-9/28!