Question

The measure of a vertex angle of an isosceles triangle is 120° and the length of a leg is 8 cm. Find the length of a diameter of the circle circumscribed about this triangle.

Answer in CM, please. Thanks!

Answer 1

16cm

Explanation:

To find the diameter we must first find the radius and multiply by 2.

The isosceles triangle that has the length of a leg to be 8cm and a vertex angle of
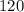`120\degree` that has been circumscribed is shown in the attachment.

We draw a line from the vertex of the isosceles triangle that bisects the base through the center O of the circle.

This implies that
`m\angle OAC=60\degree`.

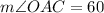Based on this
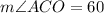`m\angle ACO=60\degree` because the two radii are equal.

It follows that:
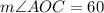`m\angle AOC=60\degree` because sum of angles in a triangle must be 180 degrees.

This means that, triangle AOC is an equilateral triangle, hence all sides are equal.

One side of this equilateral triangle happens to be the side of the leg of the isosceles triangle which is 8cm.

It follows that, the radius of the circle is 8cm.

Therefore the diameter of the circle is 16cm