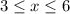ANSWER
Step-by-step explanation
The given inequality is
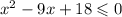
This is the same as

The corresponding equation is
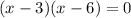
By the zero product principle,

We now plot the boundaries and test for the region that satisfies the inequality.
See attachment.
From the graph the solution is