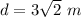Answer:
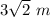
Explanation:
The perimeter of a square is:
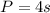
Where "s" is the lenght of a side of the square.
Then, if the perimeter of this square is 12 m, you can solve for "s" and find its value:
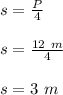
You can calculate the length of the diagonal with this formual:
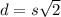
Where "s" is the lenght of a side of the square.
Substituting the value of "s" into the formula
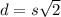 , you get that the lenght of the diagonal of this square is:
, you get that the lenght of the diagonal of this square is: