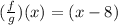Question

Which expression is equal to (f - g)(x)?

Answer 1

Answer: OPTION A

Explanation:

You need to divide the function f(x) by the function g(x):

Then:

`((f)/(g))(x)=(x^2-11x+24)/(x-3)`

Now, you need to simplify:

Factor the numerator. Find two numbers whose sum be -11 and whose product be 24. Theses numbers are -8 and -3. Then you get:

`((f)/(g))(x)=((x-8)(x-3))/(x-3)`

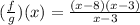
Remember that:

`(a)/(a)=1`

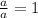
Then, you get that the expresson that is equal to
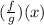`((f)/(g))(x)` is:

`((f)/(g))(x)=(x-8)`

Answer 2

A. x-8

EXPLANATION

The given functions are:

`f(x) = {x}^(2) - 11x + 24`

We factor this to get,

`f(x) = (x - 8)(x - 3)`

and

`g(x) = x - 3`

`( (f)/(g) )(x) = (f(x))/(g(x))`

`( (f)/(g) )(x) = \frac{ {x}^(2) - 11x + 24}{x - 3} \: for\: x \\e3`

`( (f)/(g) )(x) = ((x - 8)(x - 3))/(x - 3)`

Cancel the common factors to get,

`( (f)/(g) )(x) = x - 8`