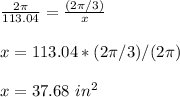Question

What is the area of a sector with a central angle of (2pi/3) radians and a diameter of 12 in?

Answer 1

The area of the sector is
`37.68\ in^(2)`

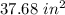
Explanation:

step 1

Find the area of the circle

The area of the circle is equal to

`A=\pi r^(2)`

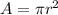
we have

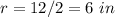`r=12/2=6\ in` ----> the radius is half the diameter

substitute

`A=(3.14)(6)^(2)`

`A=113.04\ in^(2)`

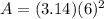
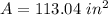
step 2

Find the area of a sector with a central angle of (2pi/3)

Remember that

The area of
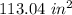`113.04\ in^(2)` subtends a central angle of
`2\pi \ radians`

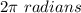
so

by proportion

Let

x----> the area of the sector

`(2\pi)/(113.04)=((2\pi/3))/(x)\\ \\x=113.04*(2\pi/3)/(2\pi)\\ \\x=37.68\ in^(2)`