Question

What is (a+b)(a-b) equal

Answer 1

Answer:a squared-b squared

Explanation:

Answer 2

`(a+b)(a-b)=a^(2) -b^(2)`

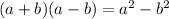
Explanation:

This is a example of remarkable identities.

We know that the result of multiplication is called product and the values ​​that multiply are called factors.

We call remarkable identities to certain algebraic expressions with binomial products very frequent in the calculation.

For this example, we got a Product of the sum for the difference of two binomials.

`(a+b)(a-b)`

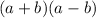
The product of the sum for the difference of two binomials is equal to the square of the first quantity, minus the square of the second.

`(a+b)(a-b)=a^(2) -b^(2)`

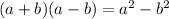
Demostration:

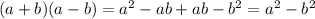
`(a+b)(a-b)= a^(2) -ab+ab-b^(2)=a^(2) -b^(2)`

.