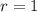Answer:
(a)
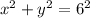
(b)
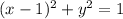
Explanation:
Remember that to convert from polar to rectangular coordinates you must use the relationship:
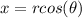
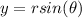

In this case we have the following equations in polar coordinates.
(a)
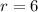 .
.
Note that in this equation the radius is constant, it does not depend on
 .
.
As
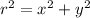
Then we replace the value of the radius in the equation and we have to::
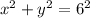
Then
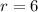 in rectangular coordinates is a circle centered on the point (0,0) and with a constant radius
in rectangular coordinates is a circle centered on the point (0,0) and with a constant radius
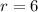 .
.
(b)
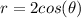
The radius is not constant, the radius depends on
 .
.
To convert this equation to rectangular coordinates we write
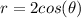 Multiply both sides of the equality by r.
Multiply both sides of the equality by r.
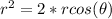 remember that
remember that
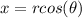 , then:
, then:
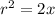 remember that
remember that
 , then:
, then:
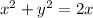 Simplify the expression.
Simplify the expression.
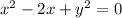 Complete the square.
Complete the square.

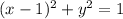 It is a circle centered on the point (1, 0) and with radio
It is a circle centered on the point (1, 0) and with radio