Question

Plsssssssss helpppppp asapasap!

Answer 1

Explanation:

-8

Answer 2

Answer: First option.

Explanation:

We need to remember that:

`\sqrt[n]{a^n}=a`

`a^{(m)/(n)}=\sqrt[n]{a^m}`

And, according to the Power of a power property we know that:

`(a^m)^n=a^((mn))`

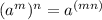
Knowing this, we can descompose 32 into its prime factors:

`32=2*2*2*2*2=2^5`

Then we can rewrite the expression as:

`=\sqrt[5]{(-32)^3}\\\\=\sqrt[5]{(-2^5)^3}`

Finally, simplifying the expression, we get:

`=\sqrt[5]{(-2)^(15)}\\\\=(-2)^3\\\\=-8`

This matches with the first option.