Question

Help please? I can’t figure out how to find the value of each trig ratio.

Answer 1

51.34

Explanation:

First, things first, identify the opposite, adjacent, and hypotenuse.

Since you are trying to find the value of x, the length measuring 4 is the adjacent because it is one of the lengths that creates that angle measure you are trying to find. 5 is the opposite because the angle is on the opposite side of the length. The
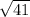`√(41)` is the hypotenuse.

Now, which trig equation do you want to use?

sin(x) = opposite / hypotenuse

cos(x) = adjacent / hypotenuse

tan(x) = opposite / adjacent

Let's first try solving with sine.

sin(x) = 5/
`√(41)`

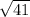
Since you want to find the angle, you have to use the
`sin^(-1) ((5)/(√(41)) )=x`

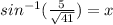
Plug it into your calculator, then you should get something like this: 51.34019175.

That is the angle measurement of x.

Let's use cosine.

cos(x) = 4/
`√(41)`

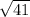
Again, since you want to find the angle, you have to use the
`cos^(-1) ((4)/(√(41)) )=x`

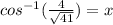
Plug it into your calculator, then you should get something like this: 51.34019175.

You realize that it gave the same answer, right? Yep, let's also do tangent.

tan(x) = 5/4

Again, since you want to find the angle, you have to use the
`tan^(-1)((5)/(4)} )=x`

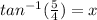
Type it into the calculator and you should get 51.34019175 again!